Hình 3.3 so sánh quan hệ ứng suất – biến dạng của ba dạng cốt thép. Trong khi tất cả các cốt thép, về bản chất, đều có cùng độ cứng (mô đun đàn hồi) xuất phát, cường độ của thép dùng cho dự ứng lực lại lớn hơn rất nhiều so với cốt thép thường.
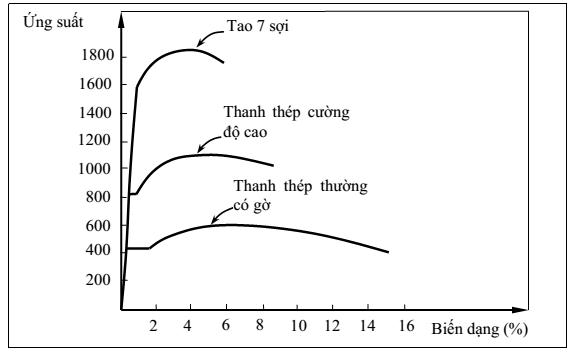
Hình 3.3 Quan hệ ứng suất – biến dạng của các dạng cốt thép khác nhau
Quan hệ ứng suất – biến dạng của cốt thép dự ứng lực có thể được lấy gần đúng theo phương trình:
fp = Ep εpf ≤ fpy (3.1)
Đối với các tao và sợi không có thềm chảy, “cường độ chảy” tương đương được định nghĩa ứng với biến dạng 1% (Hình 3.4). Tỷ số giữa cường độ chảy dẻo, fpy , với cường độ tới hạn, fpu , cho các loại thép dự ứng lực khác nhau được cung cấp trong Bảng 3.3.
Bảng 3.3 Các giá trị phổ biến của fpy / fpu
|
Kiểu bó dự ứng lực
|
fpy/ fpu
|
|
Tao thép có độ chùng thấp
|
0,90
|
|
Tao thép được khử ứng suất dư
|
0,85
|
|
Các thanh dự ứng lực trơn
|
0,85
|
|
Các thanh dự ứng lực có gờ
|
0,80
|
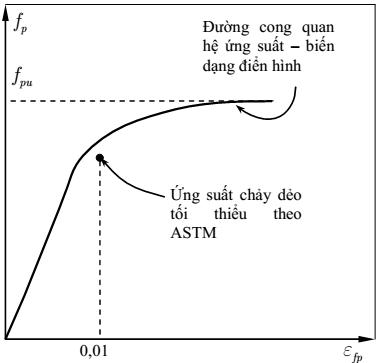
Hình 3.4 Ứng suất chảy dẻo tương đương cho cốt thép dự ứng lực
Một dạng đường cong thể hiện quan hệ ứng suất – biến dạng của các tao dự ứng lực (Hàm Ramberg – Osgood sửa đổi) có dạng:
fp = Ep εpf { A + (1-A)/ [ 1 + (Bεpf)C]1/C} ≤ fpu
Hình 3.5 Hàm Ramberg – Osgood sửa đổiNhư có thể thấy trên Hình 3.5, hàm này chứa hai đường thẳng và một đường cong chuyển tiếp và được xác định bởi 4 hằng số. Nếu có đường cong quan hệ ứng suất – biến dạng thực tế của tao thép đang nghiên cứu thì 4 hệ số của công thức (3.2) có thể được xác định như sau:
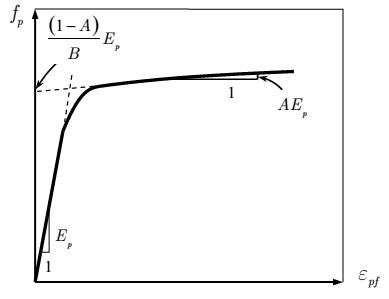
1. Biểu diễn quan hệ ứng suất – biến dạng bởi hai đường thẳng được nối bằng một đường cong.
2. Xác định Ep
từ độ dốc của đoạn thẳng đầu tiên.
3. Xác định A từ độ dốc của đường thẳng thứ hai. Độ dốc này chính là AEp .
4. Xác định B từ giao của đường thẳng thứ hai với trục fp . Giá trị của fp tại điểm giao chính là Ep (1 – A)/ B .
5. Xác định C bằng cách thử dần để tìm được đường cong chuyển tiếp thích hợp. Giá trị lớn của C sẽ cho đường cong có độ cong nhỏ.
Đối với các tao có độ chùng thấp với dạng thích hợp sẽ là fpu =1860 MPa , biểu thức cho quan hệ ứng suất – biến dạng là
f p = 200 x103 εpf { 0,025 + 0,975/[1+(118εpf)10]0.1} ≤ 1860 MPa
Trong khi đó, cho các tao thép được khử ứng suất dư với fpu = 1860 MPa , biểu thức cho cho quan hệ ứng suất – biến là
f = 200 x103 εpf { 0,03+ 0,975/[1+(121εpf)6]0.167} ≤ 1860 MPa
Các hệ số của các biểu thức (3.3) và (3.4) đã được chọn sao cho đường cong chuyển tiếp đi qua điểm “cường độ chảy” thấp nhất quy định ứng với biến dạng bằng 1%. Đường cong quan hệ ứng suất – biến dạng thực tế của các tao thép nằm ở đâu đó phía trên các đường cong này.